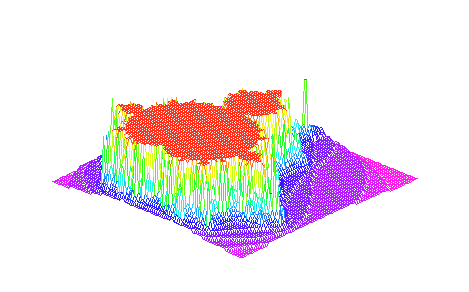
Diese Routine stammt von John Oprea und vermeidet auf intelligente Weise hohe Berechnungszeiten, indem das Fraktal mittels plot3d und dessen Farboption color dargestellt wird. Dadurch gelingt es auch, die Mandelbrot-Menge in der Ebene - und nicht im Raum - darzustellen. Würde man versuchen, mittels plot ein Fraktal anzuzeigen, so wären alle Punkte der Menge in einer Liste abzuspeichern, da Punkte in Maple V nicht direkt gesetzt werden können, wie beispielsweise in vielen Programmiersprachen mit PutPixel möglich. Die Nutzung einer Liste aber ist sehr speicheraufwendig und kann auch zum Absturz Maples (bzw. zum Abbrechen der Berechnung) führen.
# The Mandelbrot set # # 2D display coding by John Oprea, oprea@math.csuohio.edu > restart: with(plots): > mandelbrot:=proc(x, y) > local c, z, m; > c:=evalf(x+y*I); > z:=c; > for m to 30 while abs(z) < 2 do > z:=z^2+c > od; > m > end: > plot3d(0, -2 .. 0.7, -1.2 .. 1.2, orientation=[-90,0], > grid=[250, 250], style=patchnogrid, > scaling=constrained, color=mandelbrot);

(Die Bezeichnungen entstammen dem Buch Fractals for Windows von Tim Wegner, Bert Typler, Mark Peterson, und Pieter Branderhorst, The Waite Group.)
> plot3d(0, --0.83561 .. -0.78523, 0.15559 .. 0.19343, orientation=[-90,0], > grid=[250, 250], style=patchnogrid, scaling=constrained, > color=mandelbrot);

eingesetzt, wobei anfänglich z[0]=0 gesetzt wird. Die Berechnung nach obiger Formel wird nun für jedes c beliebig oft durchgeführt, es entsteht für jedes c eine Zahlenfolge z[0], z[1], z[2], usw. Nach jeder Iteration wird geprüft, ob sich z[n+1] innerhalb eines bestimmten Radius um den Ursprung befindet, hier setzen wir den Radius gleich 2.
> restart: > MandelbrotOrbit:=proc(x, y, iter) > local c, z, pts; > pts := NULL; > c:=evalf(x+y*I); > z:=0; > to iter do > pts := pts, [Re(z), Im(z)]; > z:=z^2+c > od; > [pts] > end:Betrachten wir die Zahlenfolge für c = 0+i für 10 Iterationen:
> MandelbrotOrbit(0, 1, 10);
[[0, 0], [0, 1.], [-1., 1.], [0, -1.], [-1., 1.], [0, -1.], [-1., 1.],
[0, -1.], [-1., 1.], [0, -1.]]
Diese Zahlenfolge verhält sich periodisch und wechselt bei n > 1 zwischen -1+i und -i. c=i ist also Teil der Mandelbrot-Menge.
c=0.5+0.3i:
> MandelbrotOrbit(0.5, 0.3, 10); [[0, 0], [.5, .3], [.66, .60], [.5756, 1.0920], [-.36114864, 1.55711040], [-1.794164458, -.824696607], [3.038901609, 3.259282682], [-.888000612, 20.10927877], [-403.0945476, -35.41410371], [161231.5556, 28550.76423]]Mit der Zahl 3.038901609 + 3.259282682i
> abs(3.038901609 + 3.259282682*I);
4.456214379
verläßt der Orbit den Radius 2. c=0.5+0.3i ist also nicht Teil der Mandelbrot-Menge. Folgende Graphik macht den Sachverhalt anschaulich:
> with(plots):
> xyranges := x=-2.5 .. 2.5, y=-2.5 .. 2.5:
> plotoptions := style=line, symbol=POINT, scaling=constrained:
> p1 := plot(MandelbrotOrbit(0.5, 0.3, 10), xyranges,
> plotoptions, color=navy):
> p2 := plot(MandelbrotOrbit(0.2, 0.5, 100), xyranges,
> plotoptions, color=black):
> p3 := plot(MandelbrotOrbit(0, 1, 100), xyranges,
> plotoptions, color=maroon):
> radius := implicitplot(x^2+y^2=4, xyranges):
> display({p1, p2, p3, radius}, axes=box);
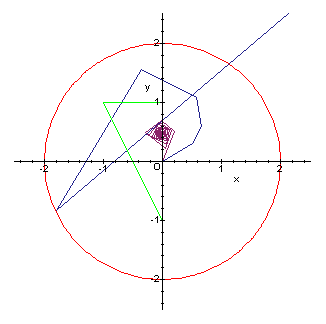
Da nicht eine unendliche Anzahl von Iterationen pro Punkt durchgeführt werden kann, um zu bestimmen, ob dieser Punkt zur Mandelbrot-Menge gehört oder nicht, begrenzt man die Anzahl der Iterationen auf einen endlichen Wert n (sog. Abbruchwert). Es ist also nicht sicher, ob ein Punkt, der nach n Iterationen innerhalb des Radius 2 blieb, ihn nach n+1 Iterationen nicht doch noch überschreitet.
In der Prozedur mandelbrot fehlt die anfängliche Zuweisung z = 0, dieses wird übergangen und statt dessen direkt z = c gesetzt.
Verschiedene Teile der Mandelbrot-Menge können durch Ändern des zweiten und dritten Argumentes der plot3d-Anweisung erforscht werden.
style=patchnogrid zeichnet die Fläche mit schattierten, rechteckigen Feldern, aber ohne ein Gitternetz, dieses ist die beste Stiloption für den Graphen.
> restart: > mandelbrot:=proc(x, y) > local z, m; > z:=evalf(x+y*I); > for m from 0 to 30 while abs(z) < 2 do > z:=z^2+(x+y*I) > od; > m > end: > plot3d(mandelbrot, -2 .. 0.7, -1.2 .. 1.2, grid=[150, 150]);