Projekt: Die Mandelbrot - Dimension

6.1.98
Dieses Projekt wurde erarbeitet von Robert Rost und Martin Nickel, Kurs
13, bei dem Fachleherer für Informatik Herrn Böttcher.Mit unserer Arbeit haben wir
die Absicht gehabt eine Einführung in die abstrakte und fraktale Dimension zu
erstellen anhand von drei Beispielen: Die Mandelbrotmenge, Juliamenge und das Feigenbaummodell.
Letzteres wurde benannt nach dem Physiker Mitchell Feigenbaum (1945-),

der sich in den siebziger Jahren mit der Periodenverdoppelung
quadratischer Funktionen beschäftigte.Dies ist der Feigenbaum :
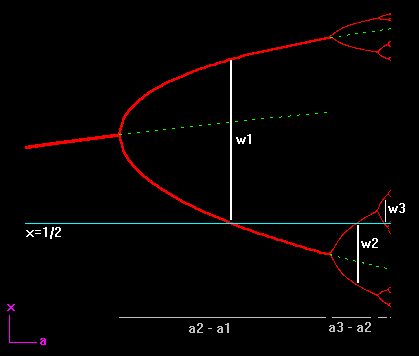
In diesem Zusammenhang seien noch die universellen Feigenbaumkonstanten erwähnt:
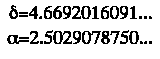
Sie ergeben sich aus einem Grenzprozeß bezüglich des Verhältnisses der
Bifurkationspunkte bzw. bezüglich der kleinsten Abstände eines Orbits.
Bei unserer Entwicklung dieses Projektes in der Hoffnung auf eine brauchbare
Lösung und Darstellung der Aufgabe, stießen wir auf verschiedene Probleme.
Zum Beispiel hatten wir Probleme unsere sowohl in Java, als auch in Turbo Pascal
geschriebenen Programme ordnungsgemäß zum "Laufen" zu bringen mit einer visuell sichtbaren
Graphikausgabe.Mittlerweile sollte das Problem gelöst sein und das Programm sollte laufen.
Ein anderes viel Merkwürdigeres Problem,das erst nach sehr langer
Bearbeitung dieser Web-Page zutage trat war das Unterschiedliche Ausgabeformat je nachdem,
welchen Browser wir benutzt hatten um diese Seite zu bearbeiten. Im Moment ist diese Seite in
ihrem Format auf den Internet Explorer eingestellt, so daß es am besten wäre diesen
zu benutzen. Sollte der User allerdings keine andere Möglichkeit als z.B. Netscape
haben, so bitten wir um Entschuldigung für die teils unharmonische Anordnung der Links
bzw. Icons.
Wie unten noch einmal angeführt befindet sich das geforderte
Ablaufprotokoll direkt am Java-Programm Mandelbrot.java.
Zuletzt sei noch erwähnt, daß wir unsere Informationen und Programmtexte
zusammengestellt und bearbeitet haben auf dem Hintergrundwissen folgender
Bücher:
"Informatik für die Sekundarstufe II" Band 1 von Klett
"Java 1.1 : schnell und sicher zum Ziel" von Paul Schulz
"Java : Objektorientiert programmieren für das WWW" von Oliver Bouchard
Zudem mußten wir auch auf die Informationsquelle des Internets zurückgreifen.
Jetzt wo die Formalitäten endgültig geklärt sind , können wir in die tieferen
Details gehen :
Wichtig für die Erfassung des fraktalen Gedanken ist der Begriff der
Dimension. Die Spur der Brownschen Bewegung, die ein Teilchen hinterläßt,
kann man aufzeichnen, indem
man aufeinanderfolgende Positionen markiert und sie durch physikalisch irreale
Strecken verbindet (d.h. die Strecken haben physikalisch keine Bedeutung).
Beobachtet man dieses Verhalten nur lange genug und mit hinreichender
Genauigkeit, so füllt diese Spur schließlich die ganze Ebene aus. Es drängt
sich hier unweigerlich der Gedanke auf, daß diese sonderbare Kurve in gewissem
Sinne die Dimension einer Ebene hat. "Topologisch" gesehen hat die Kurve die
Dimension eins. Da sie jedoch praktisch die Ebene ausfüllt, ist sie
fraktal von der Dimension zwei.
Man sieht, daß die Definition einer Dimension ausschließlich über die Anzahl
der Koordinaten keine befriedigende Lösung ergibt. Mandelbrot (1977) dachte deshalb
über geeignete Definitionen nach.
Er unterscheidet zwei Definitionen, die beide jeder Menge des
Euklidischen Raumes 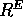 eine reelle Zahl zuordnen, nämlich die topologische
Dimension
eine reelle Zahl zuordnen, nämlich die topologische
Dimension 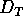 und die Hausdorff-Besicovitsch-Dimension D.
Im üblichen Euklidischen Raum
und die Hausdorff-Besicovitsch-Dimension D.
Im üblichen Euklidischen Raum 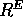 ist sowohl
ist sowohl  als auch D nicht
kleiner als Null und höchstens gleich E. Im Unterschied zu
als auch D nicht
kleiner als Null und höchstens gleich E. Im Unterschied zu 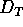 ist D
nicht immer eine ganze Zahl.
ist D
nicht immer eine ganze Zahl. 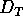 und D stimmen also nicht notwendigerweise
überein.
Sie genügen immer der
Szpilrajn-Ungleichung:
und D stimmen also nicht notwendigerweise
überein.
Sie genügen immer der
Szpilrajn-Ungleichung: 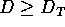 .
Da es zunächst keinen Begriff gab, der diese Mengen bezeichnete, definierte
Mandelbrot das Fraktal: '' Ein Fraktal ist nach Definition eine Menge, deren
Hausdorff-Besicovitsch-Dimension echt die topologische Dimension übersteigt
(
.
Da es zunächst keinen Begriff gab, der diese Mengen bezeichnete, definierte
Mandelbrot das Fraktal: '' Ein Fraktal ist nach Definition eine Menge, deren
Hausdorff-Besicovitsch-Dimension echt die topologische Dimension übersteigt
(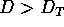 ).''
Mandelbrot nennt D eine Fraktale Dimension.
).''
Mandelbrot nennt D eine Fraktale Dimension.
Wichtig für den Zusammenhang zwischen den Fraktalen und der
powerspektralen Untersuchung in dieser Arbeit ist das Verständnis der Selbstähnlichkeit.
Die Euklidische Geometrie beginnt mit den einfachsten Formen, wie Geraden, Ebenen oder
Räumen. Hierbei entsteht die einfachste Physik, wenn eine gewisse Größe
(Dichte, Temperatur, Geschwindigkeit,...) auf homogene Art und Weise im
jeweiligen System verteilt ist. Diese homogene Verteilung hat nun zwei
Eigenschaften: die Invarianz gegenüber Verschiebungen und die Invarianz
gegenüber Maßstabsänderungen. Beim Übergang zu Fraktalen muß die
Invarianz modifiziert werden bzw. in ihrem Spielraum eingeschränkt sein. Die
besten Fraktale sind gerade solche, die ein Höchstmaß an Invarianz zeigen
(Mandelbrot, 1982).
Obwohl sich die verschiedenen Teile einer Brownschen Spur niemals exakt
übereinanderlegen lassen, ist es doch in statistischem Sinne möglich. Viele
Fraktale sind also in einem bestimmten Maße invariant gegenüber
Verschiebungen. Fraktale, die gegenüber Maßstabsänderungen invariant sind,
werden skaleninvariant genannt.
'' Ein Fraktal, das invariant ist gegenüber der üblichen geometrischen
Ähnlichkeit, heißt selbstähnlich bzw. self-similar''
(Mandelbrot, 1977).


 Biographie über Hr. Mandelbrot
Biographie über Hr. Mandelbrot
 Biographie über Hr. Julia
Biographie über Hr. Julia
 Zus. Erläuterung zum Mandelbrot
Zus. Erläuterung zum Mandelbrot
 Mandelbrotprogramm in Turbo Pascal
Mandelbrotprogramm in Turbo Pascal
 Die Henonkurve in Turbo Pascal
Die Henonkurve in Turbo Pascal
 Die erste Version der Juliakurve - Invers
Die erste Version der Juliakurve - Invers
 Die zweite Version der Juliakurve - nach der Abtastmethode
Die zweite Version der Juliakurve - nach der Abtastmethode
 Apfelmännchen in Java mit professionellem Kommentar
Apfelmännchen in Java mit professionellem Kommentar
 Zuletzt noch eine Gallerie
Zuletzt noch eine Gallerie
This is your personal VISITERCOUNTER

Top of Page


Constructed by Robert Rost and Martin Nickel, Jork




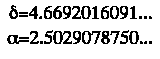
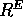 eine reelle Zahl zuordnen, nämlich die topologische
Dimension
eine reelle Zahl zuordnen, nämlich die topologische
Dimension 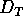 und die Hausdorff-Besicovitsch-Dimension D.
Im üblichen Euklidischen Raum
und die Hausdorff-Besicovitsch-Dimension D.
Im üblichen Euklidischen Raum 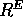 ist sowohl
ist sowohl  als auch D nicht
kleiner als Null und höchstens gleich E. Im Unterschied zu
als auch D nicht
kleiner als Null und höchstens gleich E. Im Unterschied zu 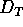 ist D
nicht immer eine ganze Zahl.
ist D
nicht immer eine ganze Zahl. 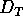 und D stimmen also nicht notwendigerweise
überein.
Sie genügen immer der
Szpilrajn-Ungleichung:
und D stimmen also nicht notwendigerweise
überein.
Sie genügen immer der
Szpilrajn-Ungleichung: 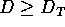 .
Da es zunächst keinen Begriff gab, der diese Mengen bezeichnete, definierte
Mandelbrot das Fraktal: '' Ein Fraktal ist nach Definition eine Menge, deren
Hausdorff-Besicovitsch-Dimension echt die topologische Dimension übersteigt
(
.
Da es zunächst keinen Begriff gab, der diese Mengen bezeichnete, definierte
Mandelbrot das Fraktal: '' Ein Fraktal ist nach Definition eine Menge, deren
Hausdorff-Besicovitsch-Dimension echt die topologische Dimension übersteigt
(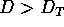 ).''
Mandelbrot nennt D eine Fraktale Dimension.
).''
Mandelbrot nennt D eine Fraktale Dimension.

